Open topic with navigation (left menu)
We occasionally receive questions about the point rating system we use in the test tool – in particular, about tests with a penalty. In the latter test type, participants are penalised with a negative score for selecting incorrect alternatives.
While tests without a penalty are useful for training and motivation, tests with a penalty are useful for exams and formal assessments that test the actual knowledge of the participants. The penalty may prevent the participants from simply guessing the correct answers – and this is a key principle behind the penalty.
Some users have pointed out that the points for different questions vary – even if the same number of correct/incorrect answers is submitted. We'll try to explain why this happens, in a non-technical way, further below, using multiple-choice and multiple-response questions as examples.
When calculating the score for each question, we use a scoring algorithm that is based on well-accepted standards for calculation of multiple-choice test results. In short, the algorithm is designed to punish participants who are trying to guess the correct answers – and to reward those with knowledge.
Extensive research was carried out for the design of the testing tool. If you would like to know more about point calculation in tests, we recommend the following literature:
A technical explanation of the algorithm can be seen below, but to fully understand how it works, you probably need higher-level math skills. Now, let's try a simplified explanation.
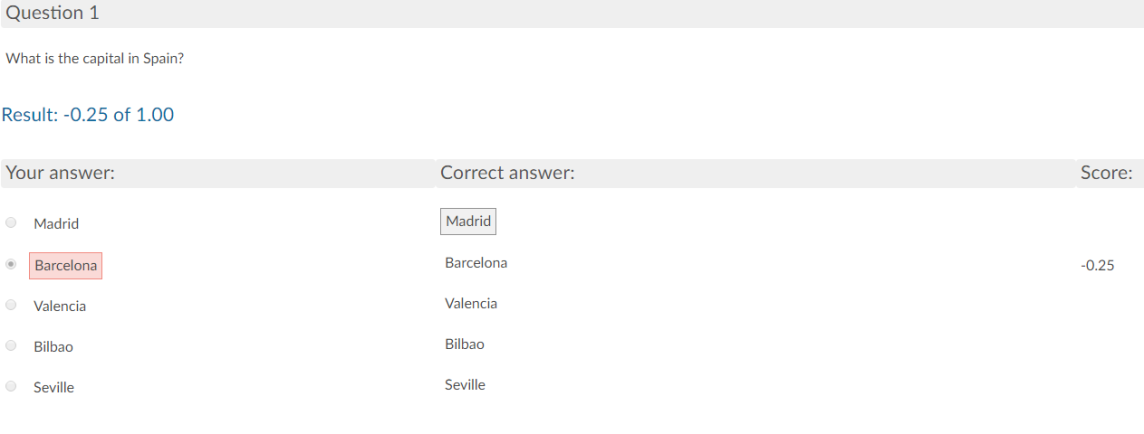
Multiple-choice questions with a penalty for incorrect answers have a fairly simple scoring algorithm. The multiple-choice question consists of one question with at least three alternatives, and the test's creator decides how many alternatives to use. Only one alternative can be selected and only one alternative can be correct. Let's say we have a question with five alternatives: 'What is the capital of Spain?'. The alternatives are:
If the participants select the correct answer, they score 1 point. If they don't answer at all (simply skip the question without selecting an alternative), they get 0 points. To prevent guessing, unanswered questions do not cause a penalty but incorrect answers are penalised with a negative score.
So far so good. Now let's take a look at how the penalty is calculated. The negative score is calculated according to the number of alternatives for the question.
The penalty is calculated as follows: -1 point divided by the number of incorrect alternatives. For a question with five alternatives, the participant will be penalised by -0.25 points (-1 point divided by four incorrect alternatives). If the question has, for example, 10 alternatives, the participant would be penalised by -0.11 points (-1 point divided by nine incorrect alternatives).

Figure 1: A multiple-choice question with five alternatives gives a negative score of -0.25 points for incorrect answers.
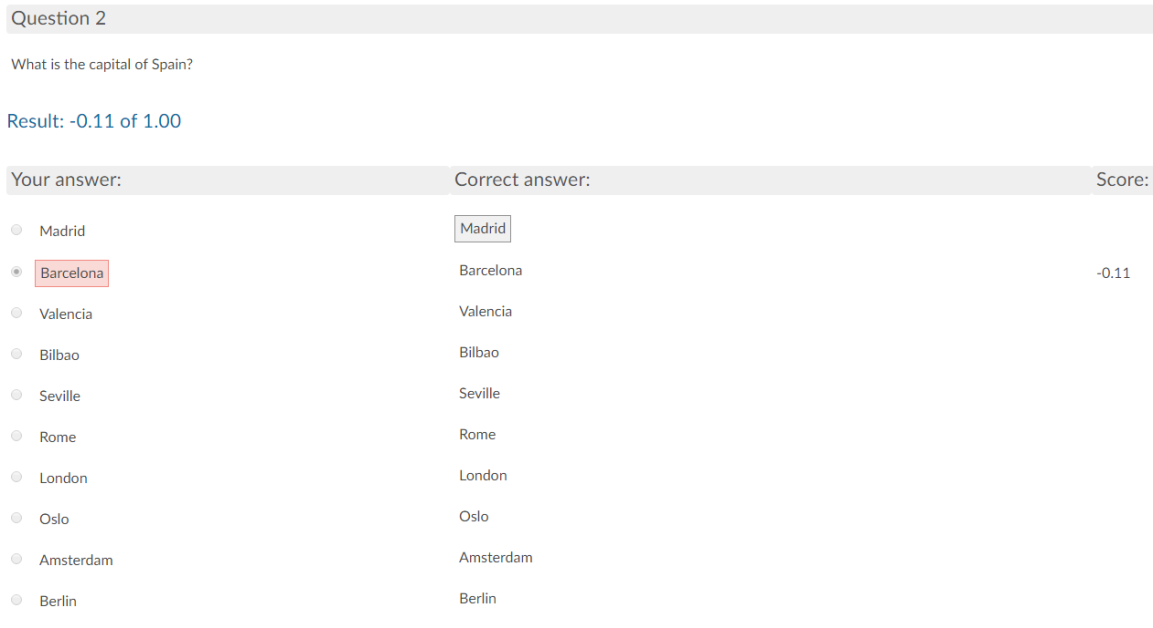
Figure 2: A multiple-choice question with 10 alternatives gives a negative score of -0.11 points for incorrect answers.
If the participants don't know the answer, they are better off leaving the questions unanswered instead of guessing. That's why you'll get 0 points for not answering the question (or for selecting all of the alternatives, which is considered the same as not answering at all).
This question type is similar to multiple choice, with one exception: the participant can select multiple alternatives, of which several may be correct. For multiple-choice questions, the algorithm is more complicated, but it follows the same logic. For the technically inclined, here is the formula:
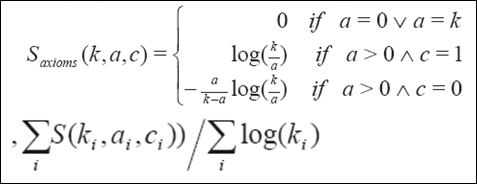
In multiple-response questions, you score points for selecting the correct alternative(s), but you are also awarded points for not selecting incorrect alternatives. To obtain the maximum score, you must select all correct alternatives and avoid selecting all of the incorrect ones.
You get a negative score if you fail to select a correct alternative or if you select an incorrect one.
The scoring is as follows:
By default, participants are awarded 1 point for correct answers. If a question has five alternatives, each question is worth 0.20 points (1 point divided across five alternatives); if it has 10 alternatives, each alternative is worth 0.10 points; and so on.
The negative score component is based on the number of alternatives for the question. The more alternatives, the less the negative score for incorrect answers.
The more alternatives a question has, the fewer points you get for an incorrect answer. This is because it is easier to guess the correct answer when there are fewer alternatives.
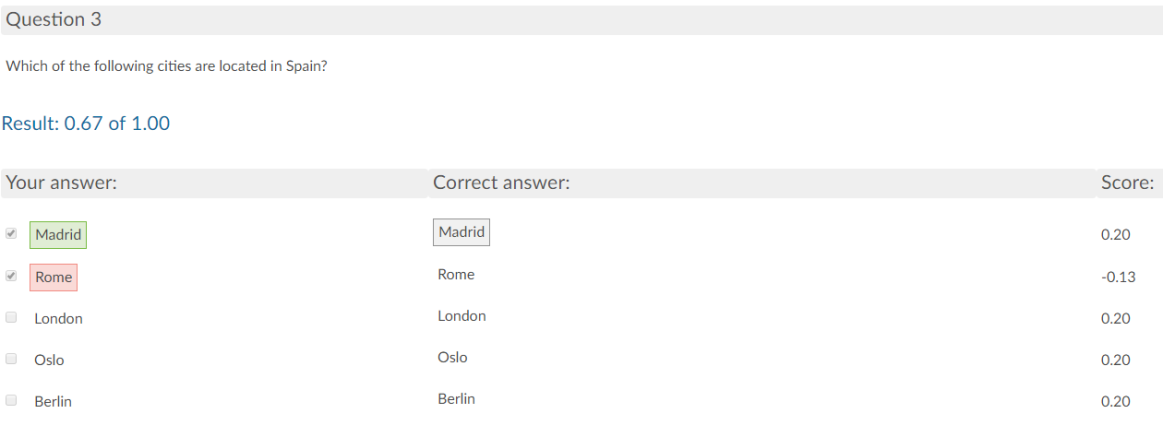
Figure 3: A multiple-response question with five alternatives gives a negative score of -0.13 points if one correct and one incorrect alternative are selected. The correct answer gives a positive score of 0.20 points. You are also given a positive score of 0.20 points for each incorrect alternative that is not selected.
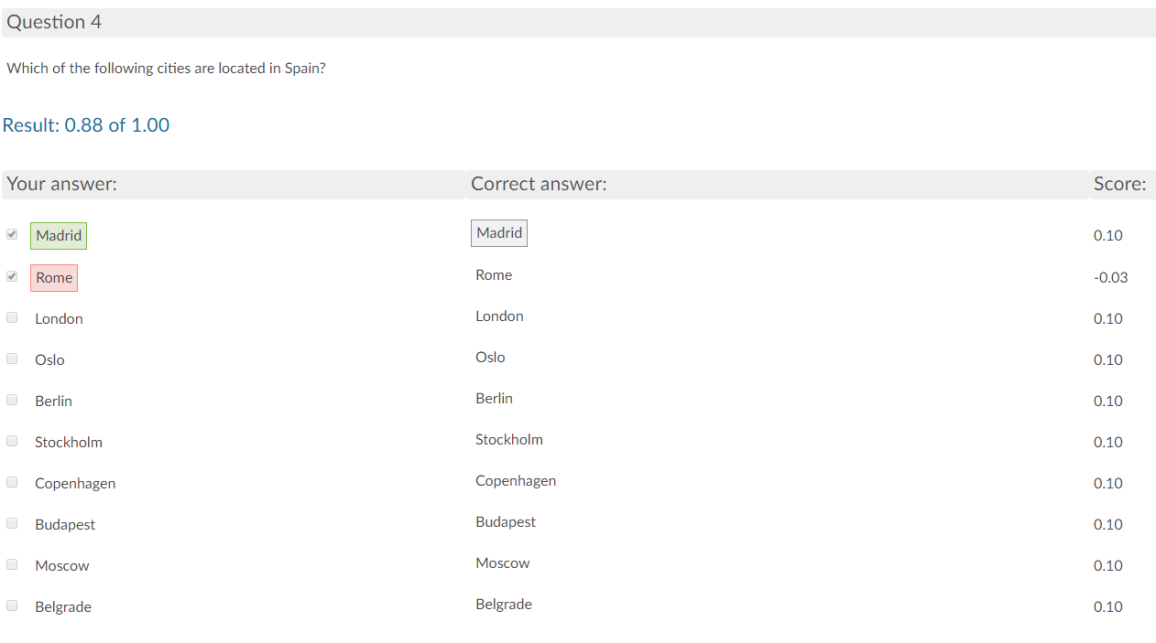
Figure 4: A multiple-response question with 10 alternatives gives a negative score of -0.03 points if one correct and one incorrect alternative are selected. The correct answer gives a positive score of 0.10 points. The negative score is lower in this example because the question has more alternatives.
The table below describes scoring algorithms that are used for various types of questions.
The Points (normal) column contains algorithms used for informal scoring method.
The Points (use negative score) column contains algorithms used for formal scoring method.
The following notations are used in pseudo-code descriptions:
| Question Type | Points (normal) Informal | Points (use negative score) Formal | References/Comments |
|---|---|---|---|
| Either/Or |
Correct: +1 p Wrong: 0 p No answer: 0 p if(a == 0) { S = 0; } else { if(c == k) { S = 1; } else { S = 0; } } |
Correct: +1 p Wrong: -1 p No answer: 0 p if(a == 0) { S = 0; } else { if(c == k) { S = 1; } else { S = 0; } } |
”Misinformation, partial knowledge and guessing in true/false tests” – Richard F. Burton “A singular Choice for Multiple Choice” – Frandsen/Schwartzbach |
| Multiple choice |
Correct: +1p Wrong: 0p No answer: 0p if(c == k) { S = 1; } else { S = 0; } |
Correct: +1p Wrong: -1/(n-1) No answer: 0p n: number of options if(c == k) { S = 1; } else { if(c == k-1) { S = 0; } else { S = -1/(k-1); } } |
|
| Multiple response |
Correct option: +1/n p Wrong option: 0 p No answer: 0p n: number of correct options specified by teacher if(a == 0 ||r a == k) { S = 0; } else { S = c/k; } |
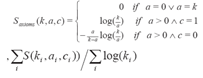
if(a == 0 || a == k) { S = 0 } else { iCor = log(k/a); iIncor = -a*log(k/a)/(k-a); sOpt = c*iCor+(k-c)*iIncor; if(sOpt >= 0) { S = sOpt/(k*iCor) } else { S = sOpt/(-k*iIncor) } } |
Must have at least 3 options Issue: “A singular Choice for Multiple Choice” – Frandsen/Schwartzbach According to [4] for the formal scoring method the total score of an answered question (S) is: S = 0 if a = 0 or a = k; otherwise Intermediate score s = (c*log(k/a)-(k-c)*((a/(k-a))*log(k/a)) Normalised total score S=s/(log(k/a)*k) if s>=0 and S=-s/(a/(k-a))*log(k/a))*k if s<0 |
| Short answer/Open answer | Same as multiple response | Same as multiple response | |
| Fill in the blank w/drop-down | The same as multiple choice – but summarised for all questions | The same as multiple choice – but summarised for all questions | |
| Fill in the blank w/text box | The same as multiple choice | The same as multiple choice | |
| Match |
Scenario 1: 1-1 (same number on each side) – Use MC x 3 (left side MC) – Max 1 point Scenario 2: 1-1 (more options to select from than targets) – Use MC x num of alternatives (left side MC) – Max 1 point Scenario 3: 1-many (sortering question) – Use MC on RIGHT side – Max 1 point |
Scenario 1*: 1-1 Always Use MC (normal) for every pair and sum results and then divide by number of pairs so that the max score is 1 p. Scenario 2: 1-1 Always Use MC (normal) for every alternative (not targets!) of the ‘select from’ set and sum results and then divide by number of alternatives in the ‘select from’ set so that the max score is 1 p. Scenario 3: 1-many Always Use MC (use negative score) for every alternative of the ‘select from’ set and sum results and then divide by number of alternatives in the ‘select from’ set so that the max score is 1 p. *) The only Scenario 1 is implemented on Phase 2 (November 2007) |
|
| Order | The same as multiple choice | The same as multiple choice | |
| Hotspot |
Text box: Use FIB Select: Use MC or MR Click: Use FIB Drag and drop: If position is shown: use MC or MR else use FIB |
Text box: Use FIB Select: Use MC or MR Click: Use FIB Drag and drop: If position is shown: use MC or MR else use FIB |
|